UEL

UEL, unification solver for EL, is a plug-in for Protégé that uses the OWL API.

Dependency

<dependency>
  <groupId>de.tu-dresden.inf.lat.uel</groupId>
  <artifactId>uel-ui</artifactId>
  <version>1.4.1</version>
</dependency>

Source code

To clone and compile the project:

$ git clone https://github.com/julianmendez/uel.git
$ cd uel
$ mvn clean install

The library, its sources and its Javadoc will be in uel-library/target, the plug-in will be in uel-plugin/target, the standalone will be in uel-standalone/target, and the release ZIP file will be in target.

To compile the project offline, first download the dependencies:

$ mvn dependency:go-offline

and once offline, use:

$ mvn --offline clean install

The bundles uploaded to Sonatype are created with:

$ mvn clean install -DperformRelease=true

and then on each module:

$ cd target
$ jar -cf bundle.jar uel-*

and on the main directory:

$ cd target
$ jar -cf bundle.jar uel-parent-*

The version number is updated with:

$ mvn versions:set -DnewVersion=NEW_VERSION

where NEW_VERSION is the new version.

Authors

Barbara Morawska, Stefan Borgwardt, Julian Alfredo Mendez

License

Apache License Version 2.0, GNU Lesser General Public License version 3

Download

version	zip	release date	Java	OWL API	Protégé
uel-1.4.1	(zip)	2024-01-06	11	4.5.26	5.5.0
uel-1.4.0	(zip)	2016-04-11	8	4.1.3	5.0.0-beta-23
uel-1.3.1	(zip)	2015-09-09	7	3.5.1	5.0.0-beta-17
uel-1.3.0	(zip)	2015-04-15	7	3.5.0	4.3
uel-1.2.0	(zip)	2012-04-30	6	3.2.4	4.1
uel-1.1.0	(zip)	2012-03-09	6	3.2.4	4.1
uel-1.0.0	(zip)	2012-01-27	6	3.2.4	4.1

Installation and use

as a plugin: in the all-in-one ZIP file, find the JAR file in directory plugin and copy it into the Protégé plugin directory (plugins).
as a library: in the all-in-one ZIP file, find the JAR file in directory library and use it as a library.
as a standalone: in the all-in-one ZIP file, find the JAR file in directory standalone and run it with java -jar uel.jar.

Release Notes

See release notes.

Support

Any questions or bug reports are truly welcome. Please feel free to contact the authors.

Tutorial - UEL as application

The following tutorial shows how to use UEL. It can be run as a standalone application …

UEL as a standalone application

… or as a plug-in inside Protégé:

UEL as a Protégé plug-in

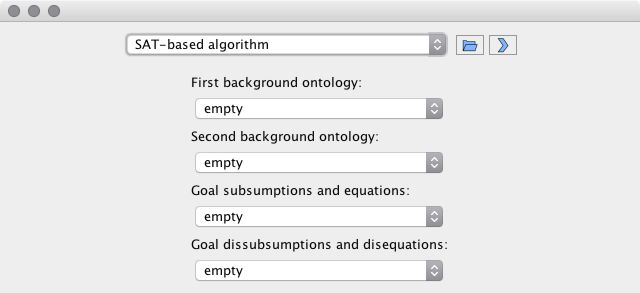
The user interface is the same in both cases. One can open the ontologies describing background knowledge and the unification problems using the “open” button of UEL, or using the Protégé menu (all ontologies to be used have to be opened in the same Protégé window).

For our example, we have opened the ontologies headinjury.owl and headinjury-dissubsumption.owl and selected them as the positive and the negative part of the (dis)unification problem, respectively. This small example consists of one equation and two dissubsumptions. A more detailed description can be found in [3]. UEL only recognizes OWL axioms of types subClassOf and equivalentClass in these input ontologies. Additionally, up to two background ontologies can be selected to provide background knowledge in the form of acyclic definitions. It is important that all OWL classes that should be shared between the selected ontologies are identified by the same IRIs in all ontologies.

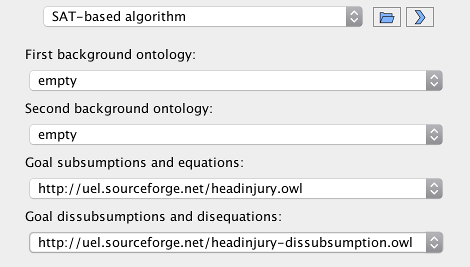
example ontologies selected in UEL

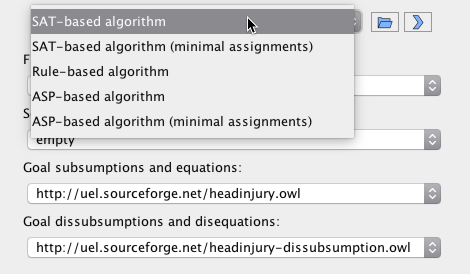
The next step is to select a unification algorithm to solve the problem. There are different advantages and disadvantages to each of them, which are discussed in the following publications. The SAT-based algorithm was developed in [4], the rule-based one in [5]. Additionally, an experimental encoding into ASP (answer set programming) has been implemented, which however requires the ASP solver clingo to be installed and available via the PATH environment variable of the JVM instance UEL is running in. Both the SAT and the ASP encoding provide the option to compute only so-called minimal assignments; for details, see [1] and [2]. It should be noted that negative constraints (dissubsumptions and disequations) are currently only supported by the SAT-based algorithm.

choose the unification algorithm

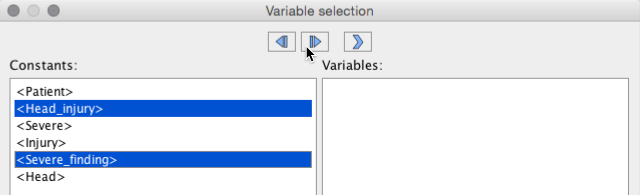
Once an algorithm has been chosen, a click on the arrow button opens a new window that allows to choose which OWL classes are supposed to be treated as variables, and which as constants. Initially, all classes are marked as constants, which are listed in the left column. Using the two first buttons, one can move classes to the second column, to designate them as variables, and back. A click on the third button starts the unification process.

select some concept names as variables

Using the arrow buttons in the next window, one can request the computation of the next unifier, as well as navigate within the set of already computed unifiers. The first and fourth button jump to the first and last unifier, respectively. In case the problem has no solution, the text “[not unifiable]” will be displayed after the first unifier has been requested. Depending on the size of the problem and the chosen unification algorithm, the computation may take a long time, even to get just the first unifier.

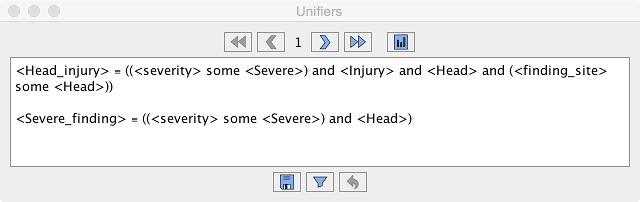
request next unifier

Using the last button in the top row, a new window is opened that contains additional information about the actual (dis)unification problem that was sent to the unification algorithm. Due to some preprocessing, additional auxiliary variables may have been introduced. This representation can be saved as a text file. In the bottom, some additional statistics about the unification process are displayed, such as the number of generated clauses for the SAT encoding.

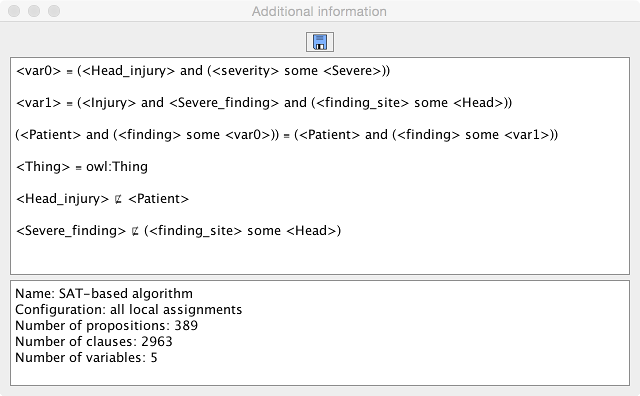
window showing extra information

Using the first button in the bottom row, one can also save the currently displayed unifier into an ontology file that contains the displayed definitions for the variables. The recognized file extensions are .krss (for KRSS format as displayed), .owl (for OWL/XML format), and .rdf (for RDF/XML format).

The second button allows to add new dissubsumptions in order to disallow some of the atoms in unifiers. For example, the substitution for Severe_finding should not contain the concept name Head.

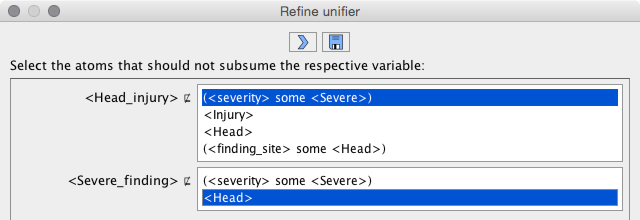
window for selecting new dissubsumptions

Using the first button in the new window, the additional dissubsumptions are added to the goal ontology and the computation of the unifiers is restarted. The second button does the same, but additionally saves the negative goal ontology to a file. In both cases, the view returns to the previous window.

The last button in the bottom row of that window allows to remove the dissubsumptions added in the previous step.

Tutorial - UEL as Java library

This small tutorial gives an example of how to use UEL as a Java library. The class AlternativeUelStarter in the uel-plugin module provides a basic OWL API interface to UEL. Its use is illustrated by the code of AlternativeUelStarterTest and is summarized by the following steps:

Construct an AlternativeUelStarter with the background ontology (an OWLOntology) as argument. Currently, only acyclic EL terminologies are supported.
Call the method modifyOntologyAndSolve with the following arguments:
The subsumptions and equations of the unification problem that is to be solved (either as an OWLOntology, or a Set<OWLSubClassOfAxiom> and a Set<OWLEquivalentClassesAxiom>). Axioms of types other than OWLSubClassOfAxiom or OWLEquivalentClassesAxiom in the input ontology are ignored. Furthermore, all OWLEquivalentClassesAxioms should contain exactly two OWLClassExpressions.
The subsumptions and equations that are to be made false by the unifiers (“dissubsumptions” and “disequations”). The input format is the same as above. Dissubsumptions and disequations are currently only supported by the SAT and ASP processors (see #4 below).
A Set<OWLClass> containing all class names that are to be treated as variables for the unification.
A String designating the unification algorithm (“processor”) to be used, as defined in UnificationAlgorithmFactory. There is an inefficient RULE_BASED_ALGORITHM, a more mature SAT_BASED_ALGORITHM (using the Sat4j library) with the option to only return “subset-minimal” solutions [1], and an ASP_BASED_ALGORITHM (using the ASP solver Clingo) that as of April 2016 is still under development. If you want to try the ASP algorithm, we can send you more detailed information on how to install Clingo and set up UEL to use it.
You get back an iterator that gives you unifiers in the form of Set<OWLUelClassDefinition> specifying a substitution for every variable. Each OWLUelClassDefinition can be converted into an OWLEquivalentClassesAxiom. It should be the case that the background ontology, extended by the OWLEquivalentClassesAxioms given by one unifier, entails all input subsumptions and does not entail any of the dissubsumptions.

AlternativeUelStarter marks all UNDEF concepts as variables by default, if you do not want this behaviour, call the method markUndefAsVariables passing false as argument before call modifyOntologyAndSolve.

AlternativeUelStarter also provides a simple command-line interface that can be accessed by starting Java directly on this class. The execution options are not documented yet, but can be found in the in the source code of the main method.

Contact

In case you need more information, please contact julianmendez.

References

[1] Franz Baader, Stefan Borgwardt, Julian Alfredo Mendez, and Barbara Morawska: UEL: Unification Solver for EL In Yevgeny Kazakov, Domenico Lembo, and Frank Wolter, editors, Proceedings of the 25th International Workshop on Description Logics (DL’12), volume 846, CEUR Workshop Proceedings, pages 26—36, 2012. ceur-ws.org Abstract BibTeX PDF Details

[2] Franz Baader, Julian Mendez, and Barbara Morawska: UEL: Unification Solver for the Description Logic EL – System Description. In Proceedings of the 6th International Joint Conference on Automated Reasoning (IJCAR’12), volume 7364 of Lecture Notes in Artificial Intelligence, pages 45—51. Manchester, UK, Springer-Verlag, 2012. DOI:10.1007/978-3-642-31365-3_6 Abstract BibTeX PDF Details

[3] Franz Baader, Stefan Borgwardt, and Barbara Morawska. Dismatching and Local Disunification in EL In Maribel Fernández, editor, Proceedings of the 26th International Conference on Rewriting Techniques and Applications (RTA’15), volume 36 of Leibniz International Proceedings in Informatics, 40–56, 2015. Dagstuhl Publishing Dismatching and Disunification in EL. DOI:10.4230/LIPIcs.RTA.2015.40 PDF Details

[4] Franz Baader and Barbara Morawska. SAT Encoding of Unification in EL In Christian G. Fermüller and Andrei Voronkov, editors, Proceedings of the 17th International Conference on Logic for Programming, Artifical Intelligence, and Reasoning (LPAR-17), volume 6397 of Lecture Notes in Computer Science (subline Advanced Research in Computing and Software Science), 97-111, 2010. Springer PDF Details

[5] Franz Baader and Barbara Morawska. Unification in the Description Logic EL Logical Methods in Computer Science, 6(3), 2010 PDF Details