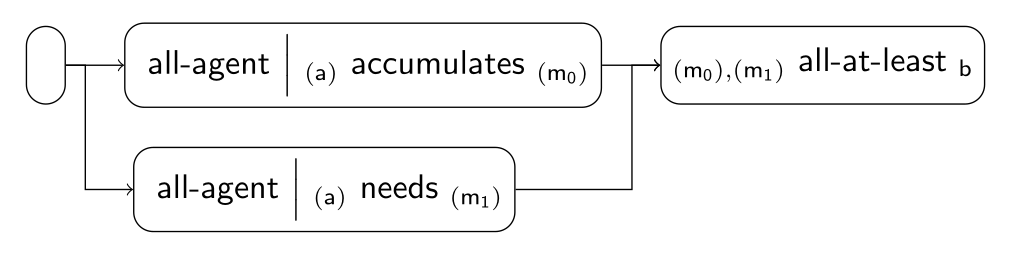
How it works
Tiles is a flexible framework for the rigorous representation of functions aimed at clarity and scalability. The framework is based on concepts of modular design, especially encapsulation, reusability, interchangeability, cohesion, low coupling, scalability, and testability.
With Tiles, we refer to the following:
- a framework where functions can be combined to create descriptions,
- a graphical representation of the framework, and
- an implementation of the framework.
Tiles
Each block, called a tile, has a name, a function, an input type, an output type, and contextual information (e.g. constants and auxiliary functions). This is denoted as follows, where α is the input type, β is the output type, and ‘name’ is the function name:
| α name β |
Graphically, this is represented as:
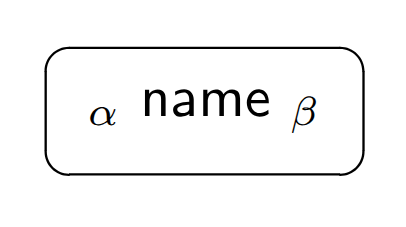
If a tile is a constant, its input type is omitted.
Types
Types in Tiles are:
- Atomic:
a(agent),r(resource),m(measure),b(Boolean). - Tuple: ⟨α_1, …, α_n⟩
- Sequence: (α)
The measure type represents quantities, such as integer numbers and floating-point numbers, and may include an undefined element (⊥).
The type annotation follows this grammar.
Primitive tiles
The primitive tiles are basic blocks, such that their definitions do not depend on other tiles.
Some tiles may be polymorphic or parametric. Polymorphic tiles are tiles such that their input or output types are generic (e.g. α, β), and they are instantiated when connected to other tiles. Parametric tiles are tiles such that their main function depends on another function φ provided as a parameter.
These are the primitive tiles.
| Function | Implementation |
|---|---|
| (α),(β) cross (⟨α, β⟩) | CrossTile |
| (α),(β) zip (⟨α, β⟩) | ZipTile |
| (α) distinct (α) | DistinctTile |
| (α) filter φ (α) | FilterTile |
| (α) map φ (β) | MapTile |
| α apply φ β | ApplyTile |
| (α) fold z using φ β | FoldTile |
Some tiles are directly derived from primitive tiles by instantiating parameters. For example:
| Function | Implementation |
|---|---|
| (α) sum φ m | SumPhiTile |
| (m) sum m | SumTile |
| (α) length m | LengthTile |
The tile
| (α) sum φ m |
is further instantiated to create
| (m) sum m |
and
| (α) length m |
Constants
The constants are a special type of tile that provide values in a deterministic way. For example, the order of elements for ‘all-agent’ and for ‘all-resources’ is always known and always the same.
| Function | Implementation |
|---|---|
| all-agent (a) | AllAgentTile |
| all-resource (r) | AllResourceTile |
Composite tiles
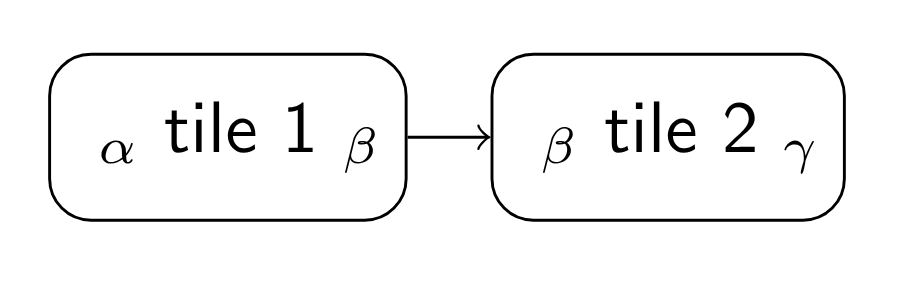
A composite tile is created by connecting two or more tiles. Assume that
| α tile 1 β |
is connected to
| β tile 2 γ |
They can be connected together to form the composite tile
| α tile 1 ⏐ β tile 2 γ |
The composite tile of the example can also be denoted as
| α tile 2 ◦ tile 1 γ |
Graphically, this is represented as:
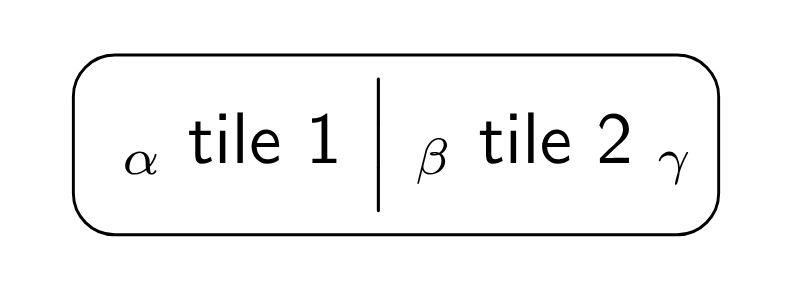
Some composite tiles receive special names because they are commonly used in multiple contexts. For example:
| Function | Implementation |
|---|---|
| (a) accumulates (m) | AccumulatesTile |
| (α) exists φ b | ExistsTile |
Pipelines
Multiple tiles can be connected to create a pipeline. Each pipeline should have one start point and one end point. To unify the generation of actors and resources, an empty tile is placed at the beginning of the pipeline.
Graphically, we can represent equity with the following pipeline: